Part 1.

1.Introduction

Recently, a new type of high-performance stainless steel with both high strength and high ductility was developed by a Chinese company. The new austenitic stainless steel termed as QN1803 employs a new metallurgical technology, which has high nitrogen and low nickel as shown in Table 1. Because of low nickel content, the material cost can be greatly reduced. The new technology can significantly reduce the cost by 15% to 20% compared with conventional S30408 stainless steel. The new material also has a high initial yield strength and tensile strength,where the initial yield strength is 40% to 50% higher than that ofconventional S30408.

The nominal yield strength of S30408 is 205 MPa, and the one of QN1803 is 440 MPa in this study. According to the definition of structural steel, steel with a yield strength beyond 420 MPa can be classified as high strength steel. Thus, QN1803 is a type of high strength stainless steel. It can be found that QN1803 shares similar properties with that of EN1.4162 as listed in Table 1, which also has a high yield strength of around twice of the S30408, while has a price around 50% of S30408. The new material also has comparable ductility as conventional stainless steel, and its elongation can achieve approximately 50%.

Corrosion resistance of QN1803 can be as good as that of S30408, and sometimes can be better than the latter. For example, cold- formed members using QN1803 has a higher pitting corrosion resistance than that of S30408. For aforementioned virtues, the new material has a great potential in civil engineering, such as roof systems, curtain wall systems and even structural members. Before application of the new material, it is necessary to obtain its constitutive relationship under monotonic loading. Meanwhile, cyclic plasticity of the material is also important for structural engineers when seismic loading is concerned.

Table 1 Chemical composition of QN1803 stainless steel
Material				Chemical Composition (Weight %)
	C	Si	Mn	P	S	Cr	Ni	Mo	Cu	N
QN1803	≤0.1	≤1.0	4.0-8.0	≤0.05	≤0.005	18.1-20.0	2.0-3.5	≤0.3	≥1.5	≤0.3
S30408	0.04	0.4	1.02	0.035	0.004	18.1	8.02	0.02	0.1	0.045
EN1.4162	0.025	0.8	4.99	0.02	0.001	21.64	1.5	0.3	0.31	0.209

A number of studies on monotonic stress-strain relationship of stainless steel were conducted , where mainly the Ramberg-Osgood model was employed. It was found that the original Ramberg-Osgood model cannot capture full-range true stress-true strain relationship of stainless steel, and a number of studies two-stage , three-stage and multistage Ramberg-Osgood models were thus developed. However, most of studies were focused on full-range engineering stress-engineering strain relationship but not true stress-true strain one.

Monotonic and cyclic plasticity of ductile metal has been extensively investigated. However, most of ductile metals have an elongation less than 30%, while elongation of the new stainless steel investigated in this study can reach as much as more than 50%.

In addition, most of previous studies were focused on small plastic strain ranges, e.g., less than 5%. For structures in regions with a high seismic risk, full-range cyclic plasticity of a material is of interest. Structures can fail due to ductile fracture or ultra-low-cycle fatigue failure in a limited number of extremely large plastic strain ranges. Under this circumstance, strain concentration can be significant, and the maximum local true strain can reach as much as 100%.

Up till now, only several studies were conducted for cyclic plasticity of stainless steel within small plastic strain ranges, and no study has been found for the new stainless steel QN1803. This material has a high potential to be employed in practice for its superior mechanical properties and low cost, especially in thin- walled structures.

2.Scope of this study

This paper aims to propose a model to well describe both monotonic and cyclic plasticity of the newly developed QN1803 stainless steel. To obtain full-range constitutive relationship of the material under monotonic loading, post- necking modification is necessary.

In this paper, two post- necking modification methods were investigated and compared to obtain full-range true stress-true strain data till fracture. A two-parameter and a three-parameter function describing full-range constitutive relationship was respectively proposed. A cyclic plasticity model with a memory surface was developed to describe cyclic plasticity of QN1803 under full-range cyclic loading. A user-defined material subroutine was also written using Fortran to implement the newly-developed cyclic plasticity model. Both experimental and numerical studies were conducted to investigate cyclic plasticity of QN1803.

For the experiments, compact specimens were designed under various loading histories, which can cover a variety of loading patterns and strain ranges. A simple method to calibrate the model parameters was also given. Through comparison of the experimental and numerical results, validity of the proposed cyclic plasticity model and parameter calibration method was proved. The proposed plasticity model can be further employed to many other metallic materials, especially for ones with high ductility.

3.Full-range monotonic true stress-true strain

3.1Post-necking modification methods

This paper aims to describe full-range cyclic plasticity of the new high-performance stainless steel QN1803. In fact, it is not so easy to obtain full-range true stress-true strain data till fracture using a monotonic tension coupon test. The main challenge is a triaxial stress state of the coupon after necking initiation.

Before necking initiation, the stress state of a material within the gage length is uniaxial tension, and this assumption doesn’t hold for the post-necking stage. Thus, a post-necking modification method is required to obtain full-range true stress-true strain till fracture. Several studies have been done to solve the above problem. Bridgman (1952) proposed a theoretical method to obtain the post-necking true stress-true strain, while it requires accurate measurement of geometrical dimensions of the necked region, which is difficult for engineers.

In fact, the cross section under post-necking stage can become elliptical, which also makes it more difficult to obtain an accurate result. Several methods using a combination of both numerical and experimental tools are proposed, and it is required to assume a monotonic hardening function of the post-necking stage. In this paper, two methods are employed, i.e., the weighted average (WA) method (Jia and Kuwamura 2014b) and the power law tangent (PLT) method (Jia et al. 2016) are both employed in this study.

It is widely accepted that necking generally occurs when the true stress is equal to tangent modulus of a true stress- true strain curve. The WA method postulates that the post- necking tangent modulus follows a linear function, and true stress can be given as follows

Fig. 1 Configuration of tension coupon

 

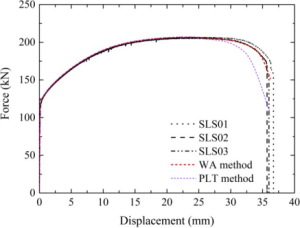Fig. 2 Comparison of load-displacement curves of two post-necking true stress-true strain modification methods

 

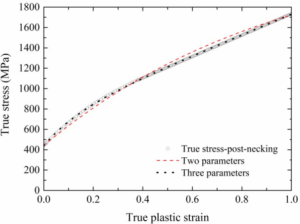Fig. 3 Full-range monotonic true stress-true strain relationship of QN1803 stainless steel

 

Table 2 Mechanical properties of QN1803 stainless steel
	Mechanical Properties					Post-necking modification parameters
Yield stress	Tensile strength	Elongation	εneck	σneck	E	w	n
(MPa)	(MPa)	(%)	(%)	(MPa)	(MPa)
440	737	71.3	38.0	1083	1.9´105	0.97	1.0
Notes: εneck and σneck are the true strain and true stress when necking initiates, respectively, E is Young’s modulus. w and n are the parameters of the weighted average method and power law tangent method, respectively

3.2Functions of full-range monotonic true stress-true strain

Three coupons with configuration shown in Fig. 1 were manufactured and pulled to rupture using an MTS testing machine. The configuration of coupons was designed based on the gauge length of the extensometer, which is 50 mm in this study, and the filleting radius is determined according to the specification, requiring a radius no less than 20 mm (GB/T 228.1-2010). Experimental results and corresponding numerical results using full-range true stress- true strain data with the aforementioned two post-necking methods are compared in Fig. 2. From the figure, it was found that the WA method can give a good evaluation of the stress-strain relationship of QN1803 stainless steel, while the PLT method cannot well describe the stress-strain relationship at the post-necking stage. This is mainly for the fact that the PLT method has an exponential expression, which will lead to no strain hardening at large strain range. The PLT method can underestimate the post-necking true stress of QN1803, and the necking deformation can be overestimated after necking initiates.

The load-displacement curves using full-range true stress-true strain data obtained by the two methods are compared in Fig. 2, indicates that the PLT method underestimates the ductility of the material due to premature necking of the tension coupon. Mechanical material properties of QN1803 stainless steel are given in Table 2, and corresponding material parameters of the two aforementioned post-necking modification methods are also listed in the table. The Young’s modulus is about 1.9105 MPa. Yield strength can reach 440 MPa, and tensile strength is 737 MPa. The yield to tensile strength of the new stainless steel QN1803 is 0.60, which is much less than 0.85.

This indicates that the material has a large residual strength after yielding, which is favorable from viewpoint of ductile design. This also indicates a high strain hardening effect, which may lead to high requirement of connected members during structural design. Elongation of the coupons in this study can reach as much as 71.3%, where the uniform elongation before necking is 38.0%.

Commonly, necking is deemed to initiate when the peak load is achieved, and the elongation of the material till the tensile strength is the uniform one, which is 38% for the QN1803 tested in this study. These values are much larger than most structural steel, indicating good ductility and energy dissipation capacity of the base metal. To facilitate application of the new material, two-parameter and three- parameter formulae to describe full-range true stress-true strain data till rupture under monotonic tension are given as follows

s = s y 0 +a1[1- exp ( – b1 ×eeq )]=440+2003[1- exp ( -1.02eeq )]	(4)
s = s y 0 +a2[1- exp ( – b2 ×eeq )]+Km  ×eeq =440+270´[1- exp ( – 6.83eeq )]+1020eeq	(5)

Since Eqs. (4) and (5) are obtained based on test results of the three coupons employed in this study, more experimental results are required to further validate the parameters of the two formulae, where a1 and b1 are material constants of the two-parameter formula, and a2, b2 and Km three-parameter ones. Full-range true stress-true strain data given by Eqs.

(4) and (5) are compared with the one using the WA method in Fig. 3, indicating good accuracy of the two-parameter and three-parameter formulae. It can also be found that the three-parameter formula gives almost the same result of the WA method, which is a bit better than that of the two-parameter one. Both of the two formulae can be employed to describe full- range true stress-true strain data of QN1803 stainless steel under monotonic uniaxial loading.

4.Introduction of combined hardening models with/without a memory surface

4.1Yield function and flow rule

Yield function describes the condition when a material yields. For ductile metal, commonly the Mises yield function is employed both for its accuracy and mathematical formation, though it can overestimate yield stress under shear-dominant loading conditions. For the combined hardening Chaboche model, there are both isotropic and kinematic hardening (KH) components.

4.2Combined hardening rule

A hardening rule describes how the yield surface evolves under the post-yielding stage. For ductile metals following the Mises yield function and the associated flow rule, formation of the backstress proposed by Armstrong and Frederick (1966) can be employed.

The generalized Armstrong-Frederick rule is also termed as Chaboche model, which gives much better evaluation of cyclic plasticity of metal than that of the Armstrong- Frederick rule for some ductile metal. There can be several backstresses in the generalized Armstrong-Frederick rule (Chaboche and Dang 1979, Chaboche and Rousselier 1983)

The generalized Armstrong-Frederick rule is also termed as Chaboche model, which gives much better evaluation of cyclic plasticity of metal than that of the Armstrong- Frederick rule for some ductile metal. There can be several backstresses in the generalized Armstrong-Frederick rule (Chaboche and Dang 1979, Chaboche and Rousselier 1983).Different backstresses can have different hardening rates, which thus can lead to better description of cyclic plasticity of ductile metal at various strain ranges. For example, there can be two backstresses.

One is expected to determine large strain range, and the other one together with the first one to define small strain range.For the combined hardening model (termed as Chaboche model in this paper), commonly there are two or three backstresses, where commonly one of them has a linear formation to describe stress-strain relationship at large plastic strain range.

4.3Memory surface

It has been found that stress can achieve a stabilized value after several constant-amplitude loading cycles, and hardening will occur again when the previous peak amplitude is exceeded. To describe this effect, memory surface is necessary to memorize loading history. Ohno (1982) proposes a formation for a memory surface in strain space as illustrated in Fig. 4, which is employed in this study.

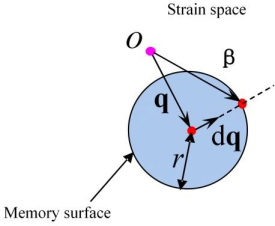Fig. 4 Memory surface in strain space

5.Calibration of model parameters

Prediction accuracy of a plasticity model is significantly affected by corresponding parameter calibration method. For structural engineers, it will be straightforward if all parameters of cyclic plasticity models can be calibrated using only tension coupon test results. A method to determine cyclic plasticity model parameters using only tension coupon test results was proposed by one of the authors (Jia and Kuwamura 2014a) based on observation during fatigue tests (Kuhlmann-Wilsdorf and Laird 1979), and good evaluation accuracy was achieved. It was postulated that IH and KH components each takes half of hardening stress for structural steel and aluminum. For the Chaboche model, full-range true stress under monotonic loading can be expressed as

si = s y 0 + R + a

where σi is true stress after post-necking modification. By postulating that ratio of the IH one to total hardening stress is constant for full strain ranges, a variable β can be defined as illustrated in Fig. 5, and IH and KH stresses under monotonic loading can be determined as follows

R = b (si -s y 0 )	(6)
a = (1- b )(si -s y 0 )	(7)

β is assumed to be a material constant, which can be calibrated based on comparison results of monotonic and cyclic tests. From Eqs. (6) and (7), it can be found that IH and KH functions can be easily obtained if value of β is known. According to Eq. , IH correlated parameters, Q and k, can be obtained based on a simple regression analysis. Likewise, KH correlated parameters, Ci and γi, can also be simply obtained based on a regression analysis.

Fig. 5 Decomposition of isotropic and kinematic hardening stress in tensile stress-strain

For structural steel and aluminum, it was found that the optimal value of β is close to 0.5. Based on comparison of monotonic and cyclic test results, an optimal value of 0.5 is obtained for QN1803 stainless steel, which is the same as those of structural steel and aluminum. The main reason may be that the cyclic hardening mechanism of these metals are basically the same, i.e., induced by crystal dislocation.

For experimental research, please see the part 2.