Part 2.

6.Experimental study

6.1Configuration of specimens

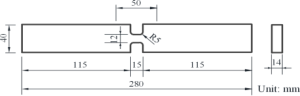Fig. 6 Configuration of compact specimens under both monotonic and cyclic loadings

Eight QN1803 stainless steel specimens with configuration shown in Fig. 6 were designed and manufactured. The configuration in the figure was designed by the authors to achieve cyclic large strain loading. A compact configuration was designed to avoid premature elasto-plastic buckling of the specimens under compression at large strain range. All specimens were cut from the same 14-mm thick stainless steel plate. The central segment has a length of 5 mm with a uniform cross-section to achieve a stress state close to uniaxial loading. The specimens were designed as compact as possible to avoid premature elastoplastic buckling under cyclic plastic loading.

Width of the central minimum cross-section is 12 mm, which is close to the thickness to avoid premature out-of-plane buckling. The central segment with a small length of 5 mm has the same cross-sectional area to produce a stress state as uniform as possible. The compact configuration was determined to avoid premature buckling under compression. Coupon test results were employed to obtain parameters of the Chaboche model with a memory surface. Manufactured specimens are shown in Fig. 7, and the tests were conducted using an MTS testing machine under room temperature at a quasi-static speed of 0.01 mm/s. Capacity of the loading machine is 500 kN, and displacement capacity is ±75 mm. Specimens were clamped to the bottom loading head, and enforced displacement was applied to the top movable loading head.

An extensometer with a gage length of 50 mm was employed to measure net deformation of the central segment as shown in Fig. 8. All the tests were controlled by displacement data of the extensometer.

Specimens were tested under different loading histories as illustrated in Fig. 9. A tension test was employed to verify the maximum tensile displacement capacity and necking initiation point of the specimen, and a compression test was to obtain instant when global buckling of the specimen occurs. Based on test results of the above two specimens, cyclic loading histories covering various strain ranges can be designed while avoiding premature buckling of specimens under compression.

Single full cycle loading history and five constant-amplitude cycles loading histories respectively shown in Figs. 9(c) and 9(d) were designed to investigate the stress stabilization effect under constant-amplitude cyclic loading. Two cycles pre- and post-necking loading histories respectively shown in Figs.

Fig. 7 Manufactured QN1803 specimens

 

Fig. 8 Test setup of specimens

 

Fig. 9 Loading histories for specimens

 

Fig. 10 Experimental results of specimens

9(e) and 9(f) were also designed to investigate cyclic plasticity of the material in strain ranges before and after necking initiation, where the necking initiation point under monotonic tension was also given in the figure. The last two loading histories, i.e., the full-range incremental and constant-amplitude loading histories respectively shown in Fig. 9(g) and 9(h), were designed investigate cyclic plasticity of the material in full strain range. Cyclic plasticity of QN1803 stainless steel can be investigated comprehensively based on the aforementioned experimental study and corresponding numerical one.

6.2Experimental results

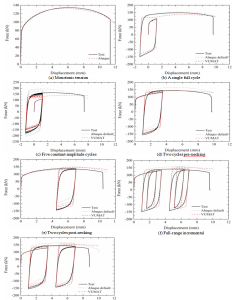
Experimental results of the specimens are shown in Fig. 10, where loads and displacement at peak and rupture points are also given. The load-displacement curves are compared since the stress state at the post-necking stage is not uniaxial. The stress and strain distribution of central uniform cross section is not uniform.

From the figure, it can be found that cyclic loading can lead to premature necking initiation. Necking initiates at 2.69 mm for the five cycles constant-amplitude loading, while the one under monotonic tension is 4.37 mm. The peak load of specimen under the five cycles constant-amplitude loading is also larger than the ones of the other specimens.

In addition, pre-necking cyclic plastic straining can also lead to premature rupture of specimens, e.g., rupture displacement of the specimen under five cycles constant-amplitude loading is 7.40 mm, which is much less than the monotonic one, which is 9.57 mm. It is interesting to find that post-necking cyclic plastic straining can even increase rupture displacements of specimens, e.g., the one under two cycles post-necking has a rupture displacement of 10.40 mm.

All specimens failed in a ductile failure mode as shown in Fig. 11 except for the monotonic compression one. Necking first initiates at middle of the specimens, and ductile rupture finally occurs.

Fig. 11 Failure mode of specimens

 

Table 3 Calibrated model parameters of the plasticity models
Chaboche model	β	C1	γ1	C2	γ2	Q∞	k	Kc
		(MPa)		(MPa)		(MPa)		(MPa)
With memory surface	0.5	922.73	6.83	510.35	0	135.05	6.83	510.35
Without memory surface	0.5	922.73	6.83	510.35	0	1001.5	1.02

7.Numerical study

7.1Finite element modeling

A three-dimensional solid model as shown in Fig. 12 was established in ABAQUS (ABAQUS, 2013) to simulate cyclic plasticity of QN1803 stainless steel. A one-eighth model was employed considering symmetric boundary conditions of specimens. Element type C3D8R with a reduced integration scheme was employed for its accuracy and efficiency. Only portion within gage length of the extensometer was simulated.

Symmetric boundary conditions were applied to the model as shown in Fig. 12(a), and mesh of the numerical model was shown in Fig. 12(b), where the central uniform part was meshed with fine elements considering strain concentration there. Enforced displacement was applied to top of the specimen. In this study, both the Chaboche models with and without the memory surface were employed in the above numerical study. The two plasticity models both employ a combined hardening rule, with both IH and KH rules.

The only difference is that there is a memory surface in strain space for the proposed plasticity model. The one without a memory surface is available in ABAQUS, and the proposed plasticity model was implemented into software using a user-defined subroutine developed in Fortran. The user- defined subroutine is termed as VUMAT in ABAQUS, which employs an explicit integration scheme. The plasticity model parameters are all calibrated through monotonic coupon test results using the aforementioned method. Values of the calibrated plasticity model parameters are given in Table 3.

Fig. 12 Boundary conditions and FE mesh of specimens

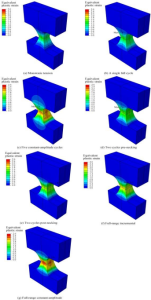
Fig. 13 Contour plots of equivalent plastic strain at instant of rupture

 

(a) Monotonic tension (b) A single full cycle (c) Five constant-amplitude cycles (d) Two cycles pre-necking (e) Two cycles post-necking (f) Full-range incremental (g) Full-range constant-amplitude

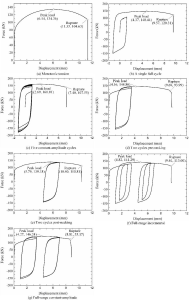
Fig. 14 Comparison of experimental and numerical results for specimens

7.2Numerical results

Equivalent plastic strain contour plots obtained from the numerical simulation were given in Fig. 13, implying extremely large plastic strain. The maximum value can reach as much as 260% for specimen under the full range constant-amplitude loading, and the maximum equivalent plastic strain of specimen under monotonic tension is 130%. The elongation of the material is 71.3% in this study, and true strain at the necked region can be much larger.

Load-displacement curves obtained from the numerical simulation were compared with corresponding experimental results in Fig. 14, where “Abaqus default” denotes the Chaboche model without a memory surface, and VUMAT denotes the proposed model with a memory surface. Based on comparison results, following observations can be found:

(1)The Chaboche model without a memory surface can give a good evaluation result for the specimen under a single full cycle loading, which is even a bit better than the proposed model with a memory surface.

(2)For the specimen under five constant-amplitude cycles loading, the Chaboche model without a memory surface greatly overestimates cyclic hardening at both tensile and compressive sides during constant-amplitude loading stage, while predicting a premature necking initiation of the specimen. The Chaboche model with a memory surface can generally give a good evaluation result for the specimen.

(3)For the specimen under two cycles pre- and post- necking loadings, the Chaboche model without a memory surface can overestimate stress at tensile side, while underestimate the one at compressive side. The Chaboche model with a memory surface can generally give a good evaluation result for the specimen.

(4)Similar conclusion to the ones under pre- and post- necking loadings can be obtained for the two specimens under full range cyclic loading histories.

It can also be found that the hardening moduli as the elasto-plastic transition zones are overestimated by the proposed model. The deviation is mainly correlated the calibration method for the cyclic plasticity model, where the model parameters are calibrated using monotonic tension coupon test results. The hardening modulus at the transition zone of the first loading cycle is much higher than those of the subsequent ones. This leads to overestimation of the VUMAT at the transition zones except the first half cycle.

8.Conclusions

A new austenitic stainless steel termed as QN1803 with high nitrogen and low nickel was recently invented, which leads to significant reduction of material cost by approximate 15% to 20%. In addition, the new material has high initial yield strength and tensile strength. This high- performance material has a high potential to be widely employed in many applications.

In this study, an experimental study on cyclic plasticity of the new high- performance stainless steel QN1803 was conducted to investigate its full-range monotonic and hysteretic properties. A combined cyclic plasticity model with a new isotropic hardening (IH) rule was proposed, and a memory surface in strain space was also employed to simulate the new high-performance material. The newly developed plasticity model was implemented into ABAQUS using a user-defined subroutine. Numerical study was carried out to capture cyclic plasticity of the new material and verify validity of the newly proposed model. Based on experimental and numerical results, following conclusions can be made.

(1)For the new high-performance stainless steel QN1803, yield strength can reach 440 MPa and it has an elongation beyond 50% in this study, indicating QN1803 has high strength and good ductility. In addition, the yield to tensile strength ratio can be as low as 0.60, implying high strain hardening effect and a high post-yielding strength potential.

(2)Both two-parameter and three-parameter formulae were proposed for full-range true stress-true strain relationship of the material, and the three-parameter one with an exponential function and a linear one gives the best evaluation accuracy.

(3)The newly proposed plasticity model with a new IH rule and a memory surface in strain space can generally well simulate full-range cyclic plasticity of QN1803 stainless steel under various loading histories.

(4)The Chaboche model without a memory surface can greatly overestimate cyclic strain hardening effect under cyclic constant-amplitude loading and underestimate stress at reversal sides under some cyclic loading histories, e.g., cyclic incremental loading.

(5)Based on comparison between numerical and experimental results, ratio of the IH component to total post-yielding hardening stress, β, can be taken as 0.5 for QN1803 stainless steel.